我喜欢通过不同方式思考事物所带来的感觉,特别是当某些模糊的想法被形式化为具体的概念时。信息论便是一个极好的例子。
信息论为我们提供了精确的语言来描述许多事物。我对事物有多少的不确信?知道问题A的答案能够为问题B提供多少信息?两组观点之间有多么相似1?当我还是孩子时便对这些念头有了简单的思索,但是信息论把这些念头变成了精确而又有效的概念2。这些概念有着非常多样的应用,从数据压缩,到量子物理,再到机器学习,以及它们之间的交叉领域。
不幸的是,信息论看起来似乎有点让人畏惧。我并不认为有什么理由使得它必须如此。事实上,许多核心概念可以完全通过图形来解释!
概率分布的可视化
在我们进入信息论的世界之前,让我们想一想如何将简单的概率分布可视化。接下来我们会需要它,并且这并不是一件难事。此外,这些把概率可视化的技巧本身也是非常有用的!
我住在加州。那儿有时会下雨,但是大部分时间是艳阳高照的!让我们假设有75%的日子是晴天。很容易得到这样一张图:

大部分日子里,我穿着T恤,但有些时候我也穿外套。假设我有38%的时间穿着外套。同样很容易得到这样一张图:
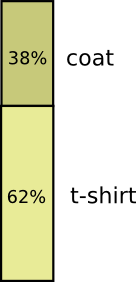
如果我想同时把他们可视化该怎么办?这很容易,只要它们互不影响——也就是说它们是独立的。比如说,我今天穿T恤还是雨衣与下周的天气如何是没有关联的。我们可以用坐标轴表示变量:

注意到水平和垂直方向上的直线一直延伸到边界。这就是独立性所表现出来的样子3!我穿外套的概率并不会因为接下来的一周将会下雨的事实而改变。换句话说,我穿外套并且下周会下雨的概率,就等于我穿外套的概率,乘上下周下雨的概率。它们并不互相影响。
当变量之间互相影响时,对于某些情形的组合会有额外的概率,同时另一些组合的概率会消失。下雨天我穿外套的概率会额外增加,因为这两者之间是有关联的,一个因素的存在会使得另一个因素更容易发生。在某个下雨天我穿外套的概率高于我在任意天气下穿外套的概率,也高于任意一天会下雨的概率。
从图形上看,一些方块区域由于得到了额外的概率而膨胀,而另一些区域由于所对应的事件不太容易同时发生而收缩。

虽然这看起来有点酷,但是对于理解到底发生了什么并没有很大的用处。
换一种方法,让我们关注某一个变量,例如天气。我们知道某一天是晴天或者雨天的可能性。对每一种情况,我们可以考虑条件概率。在晴天我有多大的可能性会穿T恤?在雨天我又有多大的可能性穿外套?

下雨的概率是25%。如果下雨,那么我有75%的几率穿外套。因此,下雨并且我穿外套的概率是25%乘以75%,大概是%19。这个概率等于下雨的概率,乘上在雨天我穿外套的概率。我们把它写成: $$\begin{aligned} p(rain, coat) = p(rain)\times p(coat|rain) \end{aligned}$$
上面这个式子是概率论最基本恒等式之一的一个简单情形: $$\begin{aligned} p(x,y) = p(x)\times p(y|x) \end{aligned}$$
我们在对概率分布进行分解,把它变成两个部分的乘积。首先我们考虑一个变量(例如天气)取某个值的可能性。然后再看另外一个变量(例如我穿的衣服)在上一个变量值给定的条件下取某个值的可能性。
选取哪个变量作为开始是随意的。我们可以先考虑我穿什么衣服,然后再考虑该条件下的天气。这可能让人觉得有点违反直觉,因为我们知道天气影响穿着是一个因果关系,反过来的话就没有这样的因果关系了,但是上述的做法仍然行得通!
让我们继续考虑一个例子。如果我们随便挑一天,在那一天我有38%的概率会穿外套。如果我们知道当天我一定会穿外套,那么那天有多大的可能性在下雨?当然,和晴天相比,在雨天我更可能穿外套,但是在加州下雨可是个稀有事件,所以折衷算来有50%的几率在下雨。因此,(在那天)下雨并且我穿外套的概率就是我穿外套的概率(38%),乘上当我穿外套时下雨的概率(50%),大概是19%。 $$\begin{aligned} p(rain, coat) = p(coat)\times p(rain|coat) \end{aligned}$$
这给了我们另外一个将上述概率分布进行可视化的视角。

注意该图中标签的意义与上一个图所表示的有些许不同:t-shirt和coat现在代表边缘概率,即不考虑天气情况时我穿哪样衣服的概率。换句话说,现在rain和sunny标签都有两个,分别对应着在穿T恤的条件下和穿外套的条件下的雨天和晴天的概率。
(你或许曾经听过贝叶斯定理。如果你想的话,可以把该定理看成是在上述两个可视化视角间进行切换的方法!)
延伸: 辛普森悖论
这些对概率分布进行可视化的技巧是有用的吗?我想是毫无疑问的!我们还要过一会儿才用这个技巧对信息论进行可视化,因此我打算先偏离一下主线,用这个技巧来探讨一下辛普森悖论(Simpson’s Paradox)。辛普森悖论是一个非常反直觉的统计情形。很难在直觉上去理解问题所在。Michael Nielsen写了一篇精彩的文章Reinventing Explanation来探究对该问题的不同解释方式。我想尝试一下使用我们之前建立的技巧来解释这个问题,
对两种不同的肾结石疗法进行临床试验。一半患者接受疗法A,另一半接受疗法B。结果显示使用疗法B进行治疗的患者存活率更高。

然而,(结果又显示)结石块较小的患者使用疗法A治疗的存活率较高,结石块较大的患者也是使用疗法A治疗的存活率较高!这怎么可能?
问题的关键在于这个实验并没有良好地进行随机化。接受疗法A进行治疗的患者更多的是具有大结石块的患者,而接受疗法B的患者更多地具有小结石块。
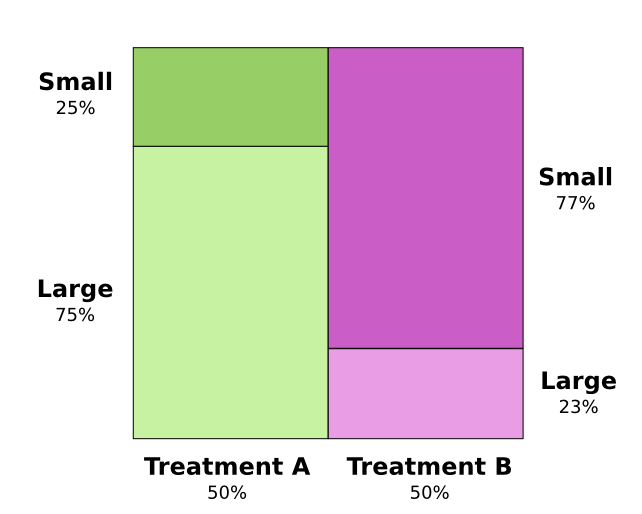
事实证明,结石块较小的患者更容易存活。
为了更好进行理解,我们可以把上面两幅图合并在一起。结果是一张表示存活率的三维图像,并且按照结石块大小进行了区域划分。

我们可以看见在大结石块和小结石块这两种情形中,疗法A都优于疗法B。疗法B看起来更好仅仅是因为它施用的对象更多地属于易治疗的群体。
编码
有了对概率进行可视化的方法,我们现在可以研究一下信息论了。
让我向你介绍一下我的假想的朋友鲍勃。鲍勃非常喜欢动物。他不停地谈论它们。事实上,他任何时候只说四个词:dog,cat,fish和bird。
几周之前,鲍勃搬到了澳大利亚(虽然他只是我想象中的虚构人物)。然后,他决定只想通过二进制码进行通讯。我从鲍勃那里收到的所有(虚构的)信息都长成这样:

为了交流,鲍勃和我建立了一套编码,一种把词映射到一个比特(bit)串的方式。
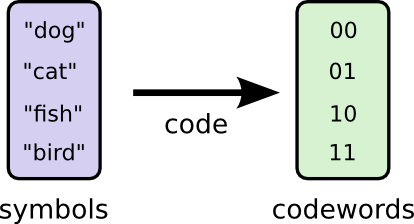
为了发送消息,鲍勃把某一个符号(单词)用相应的码字(codeword)替代,然后把这些码字串接起来形成编码字符串。

可变长度编码
不幸的是,通讯服务在假想的澳大利亚是很贵的。我必须为每一条从鲍勃那里接收到的信息中的每一个比特付出5美元。我是不是忘记说鲍勃是个话痨了?为了防止我破产,鲍勃和我决定找找看有没有办法把信息的平均长度变得短一些。
事实上鲍勃使用各个词的频率并不相同。他非常喜欢狗,总是在谈论它们。偶尔他会谈论一些别的动物,特别是他的狗喜欢追的猫,但大部分情况下他还是在提起狗。这是他的词频分布图:
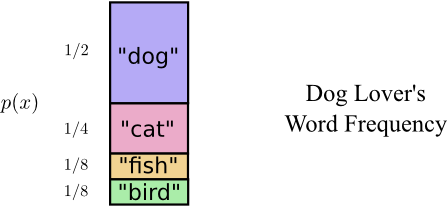
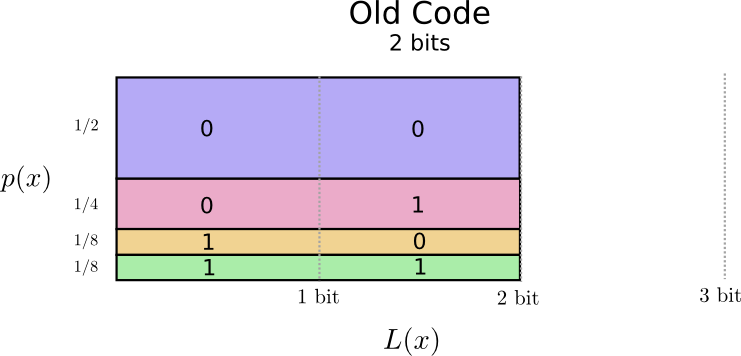
看起来有点希望。我们的旧编码为每一个词分配的码字的长度都是2个比特,无论这些词有多常用。
有一个很好的方法对编码表进行可视化表达。在下面的示意图中,我们用纵坐标来表示每个 词出现的概率$p(x)$,横坐标表示词对应码字的长度$L(x)$。注意到整幅图的面积就是我们 发送的码字的平均长度,在当前的情况下是2比特。
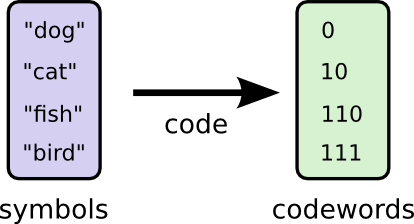
或许我们非常聪明并且提出了一种可变长度的编码方式,刻意地让较常用的词对应的码字较短。这里有一个难题是码字之间是互相竞争的——让一些码字变短会使得另一些码字变长。为了减小信息的长度,我们憧憬着让所有的码字都变短,但是我们尤其想让较常用的单词的码字变短。所以得到的编码是较常用的词有着较短的码字(比如dog),而较不常用的词对应的码字较长(比如bird)。
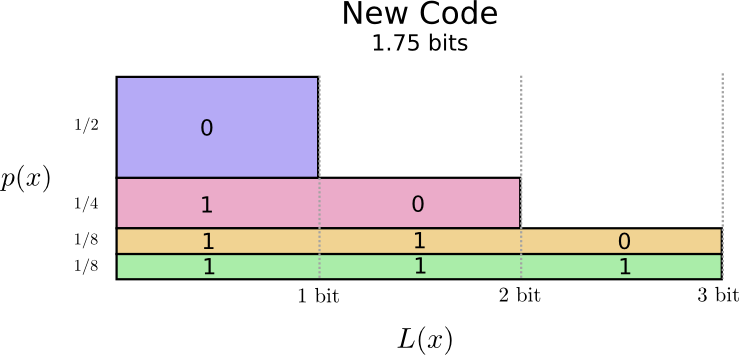
让我们把新的编码也可视化。注意到最常用的码字变得短了,虽然那些不常用的码字变长了。两相抵消,图中的面积变小了。这对应着更小的码字长度期望。现在码字的平均长度变成了1.75比特!
(你或许会想:为什么不把1也作为一个码字呢?非常不幸,这样在对编码字符串进行解码时会导致歧义。我们过会儿会讨论这件事。)
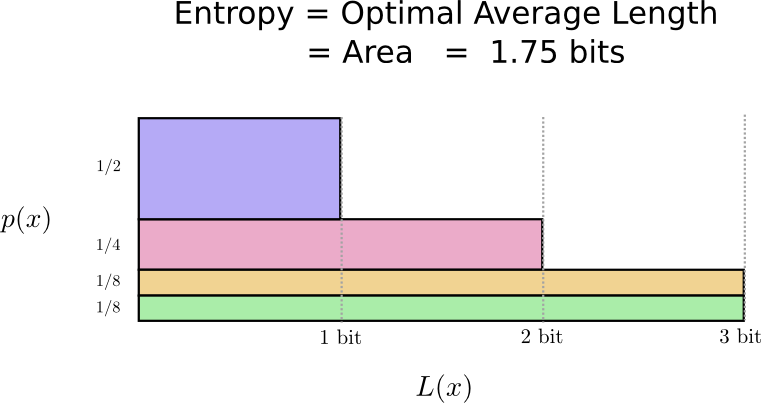
事实上这个编码是所有编码中最优的一种。对于上述的概率分布,没有任何一种编码能使得平均码字长度低于1.75比特。
总是存在这样一个基本的底限。不管我们说什么,按什么顺序说,在上述的概率分布下,都会使得我们的码字平均长度至少为1.75比特。无论我们多聪明,都不可能使得平均码字长度变小。我们把这个基本底限称为这个分布的熵(entropy)——过会儿我们会更详细地讨论它。
如果我们想弄明白这个底限存在的原因,那么最关键的就是理解码字长度之间的权衡。一旦我们弄明白该如何权衡,我们就能够知道最优的编码应该是什么样的。
码字空间
长度为1比特的码字有两个:“0”和“1”。长度为2比特的码字有四个:“00”, “01”,“10”和“11”。每多加一个比特,可用码字的数量就翻番。

我们关注的是变长编码,在这种方式下一些码字的长度比另一些码字长。我们可以用一种简单的分配方式,比如直接产生8个长度为3比特的码字,也可以做得复杂一些,例如产生2个长度为2比特的码字,然后加上4个长度为3比特的码字。是什么决定了我们可以有多少个不同长度的码字呢?
回想一下,鲍勃把他的消息中的单词用码字替代,然后把码字串接起来变成编码字符串。
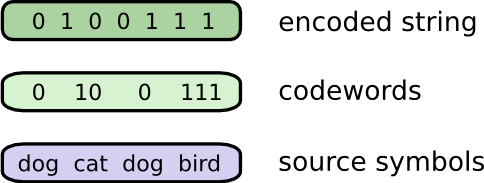
但是对变长编码进行解码时有一个小问题需要我们注意。我们如何把编码字符串分解成码字呢?当所有的码字长度一致时,方法是很简单的——只要每隔一段距离分割一下就好。但是当码字长度不一致时,我们需要仔细考虑编码字符串的内容。
我们非常希望所设计的编码有唯一的解码方式。编码中存在歧义是我们不愿看见的。如果我们有一些特殊的“码字截止”符号,事情就会容易地多。但我们做不到——我们的编码中只能有两种符号,“0”或“1”。我们只能够去观察码字串联成的序列,然后找出每一个码字的截止位置。
让编码只有唯一的解码方式是完全可以做到的。比如,假设我们有两个码字:“0”和“01”。那么对于编码字符串“0100111”,我们无法知道第一个码字是什么——它既可能是“0”,也可能是“01”4。我们希望码字拥有这样的性质:对于任意一个码字,不可能通过在它的末尾添加一些新的字符来形成新的码字5。换句话说,任何码字都不能是其它码字的前缀。这被称为前缀性质(prefix property),具有这种性质的编码叫做前缀编码。
对于前缀编码,一个有趣的发现是:每使用一个码字都会牺牲掉一些原本可用的其它码字。如果我们使用了码字“01”,我们就无法把其它以“01”为前缀的字符串作为码字。“010”或者“011010110”都没法再用了,不然就会有歧义隐患——所以我们得和这些字符串说再见了。

在所有可用的码字中,有四分之一是以“01”开头的,所以当使用“01”作为码字时,我们就损失了四分之一的码字空间。这是为使用一个长度为2比特的码字所付出的代价!这个代价所带来的影响是,其它码字的长度都必须变长。不同码字之间的长度权衡是一直存在着的。一个较短的码字会让我们损失掉更多的码字空间,使得其它的码字无法缩短。我们需要寻找的是一种合理分配各个码字长度的方法!
最优编码
你可以把寻找最优编码看成是:在有限的预算下尽可能使用较短的码字6。我们使用一个码字的代价就是牺牲掉一部分其它可用的码字7。
使用长度为0的码字的代价是1,即所有可能的码字都没法用了——如果你想使用一个长度为0的码字,这意味着你无法使用任何其它的码字,其实就是无法使用所有码字。使用长度为1的码字,比如“0”,它的代价是$\dfrac{1}{2}$,因为有一半的可用码字是以“0”开头的。使用长度为2的码字,例如“01”,相应的代价是$\dfrac{1}{4}$,因为有四分之一的码字以“01”为前缀。事实上,使用一个码字的代价随着该码字的长度增长以指数(exponentially)速度下降。

注意到如果代价是以(自然)指数速度下降,那么图中深色部分的高度和面积是一致的8,9!
我们想要使用较短的码字是因为这样能使得平均信息长度变短。每使用一个码字会使得平均信息长度增加,增加的量等于该码字的长度乘上码字的出现概率。比如说,如果我们想使用一个长度为4比特的码字,该码字的使用频率为50%,那么我们的平均信息长度就会比不使用这个码字的时候多2比特。可以画一个矩形来示意。

信息的平均长度以及使用码字所花费的代价都和码字的长度息息相关。使用一个码字所付出的代价由码字的长度所决定。而码字的长度又控制了该码字对于平均信息长度的影响。我们可以把码字的代价和对于平均信息长度的贡献放在一幅图中表示。
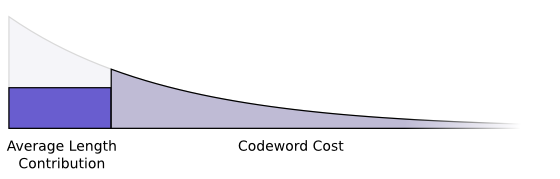
使用短的码字能够减少平均信息长度,但是会更多地消耗码字空间,而使用长的码字会增加平均信息长度,但是不会占用太多码字空间。

怎样才是使用我们有限预算的最好方式呢10?我们应该为某个词分配多少花费来产生相应的码字呢11?
正如人们会对较常使用的工具花费更多的钱一样,我们也愿意为较常使用的码字花费更多的代价。我们有一个自然而然的想法:按照词汇使用的频繁程度来为对应的码字付出相应的开支。所以,如果一个词汇使用的频率是50%,那么我们就为该词对应的码字付出50%的开支。如果一个词汇只有1%的使用概率,那么我们就只会为它对应的码字花费1%的开支,因为即使这个码字非常长我们也不怎么在乎。
这是一个非常自然的做法,但是这样做能保证编码的方式最有效率吗?确实是这样的,我将要证明它!
接下来的证明是通过图形的方式并且容易理解的,但是仍然需要动点脑子,这是整篇文章中最难的部分。读者可以直接使用结论而跳过证明的部分。
让我们画一个需要发送两个词汇的例子。词汇$a$使用的概率是$p(a)$而词汇$b$使用的概率是$p(b)$。我们使用上述的方法来分配开支,即为词汇$a$指定一个会占用$p(a)$码字空间的码字,而为词汇$b$指定一个会占用$p(b)$码字空间的码字。
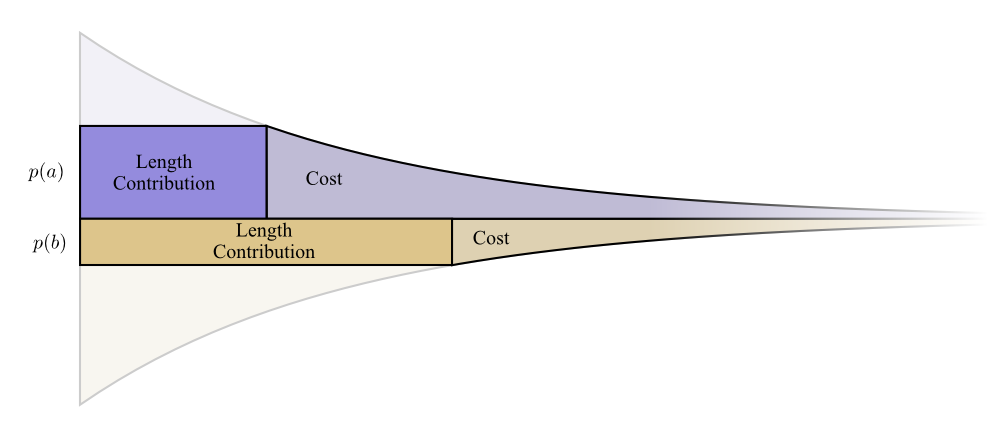
代表码字代价的边界和平均长度贡献的边界完美地重合了。这意味着什么吗?
嗯,让我们考虑一下当稍微改变码字长度时,码字代价和长度贡献会产生何种变化。如果我们稍微增加一点码字的长度,那么平均信息长度增加的量与边界的高度成一定比例,而码字代价减小的量也与边界的高度成比例12。

所以,让$a$的码字变短一些所付出的代价是$p(a)$13。同时,我们并不是同样关心所有码字的长度,我们倾注的关心程度与该码字的使用频率有关。对于词汇$a$,关心的程度就是$p(a)$。把$a$的码字变短1比特所带来的收益就是$p(a)$。
有意思的是,上述分析得到的两个导数是相同的。这意味着我们初始的预算分配方案有一个有趣的性质:如果我们有多余的预算,想要把某个码字的长度减小,那么缩短任意一个码字所带来的效果都是等效的14。最终我们真正关心的是收益/代价比——这决定了我们应该把预算投给谁。在现在的例子中,这个比例是$\dfrac{p(a)}{p(a)}$,实际上就是1。这和$p(a)$是多少无关——$\dfrac{p(a)}{p(a)}$永远是1。对于另外一个词汇我们也可以有相同的论证。所有码字的收益/代价比都是1,所以把额外的预算分配给哪个码字都一样。
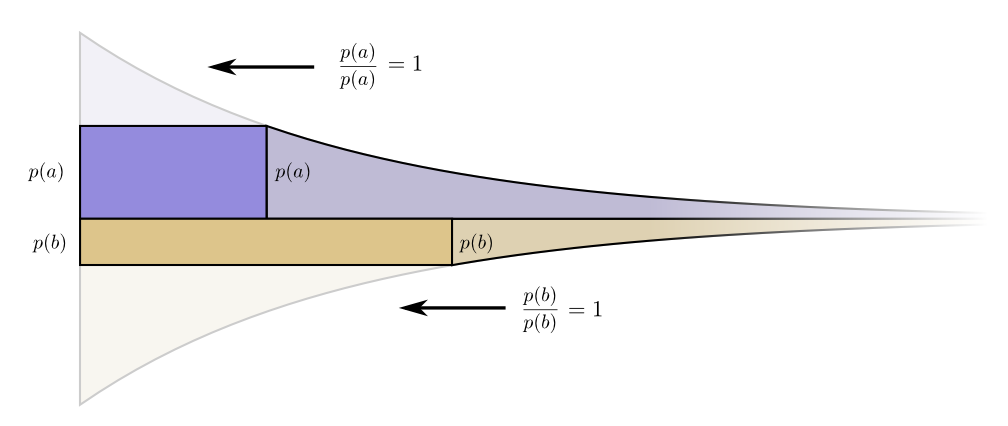
毫无疑问,我们不能改变我们的预算15。以上的论述并不能证明我们的分配方式是最优的。为了证明最优性,来考虑另一个分配方式,更多地把一些预算分配给一个码字而减少另一个码字的预算。我们把给$b$的预算减少$\epsilon$,然后投入到$a$上。这使得$a$的码字变短,而$b$的码字变长。
现在为$a$分配更短的码字所对应的代价是$p(a)+\epsilon$,而$b$的代价是$p(b)-\epsilon$。但是为它们分配更短码字的收益都还是保持不变的。这使得对$a$投入更多预算的收益/代价比为$\dfrac{p(a)}{p(a)+\epsilon}$,是小于1的。与此同时,对$b$投入更多预算的收益/代价比为$\dfrac{p(b)}{p(b)-\epsilon}$,是大于1的。
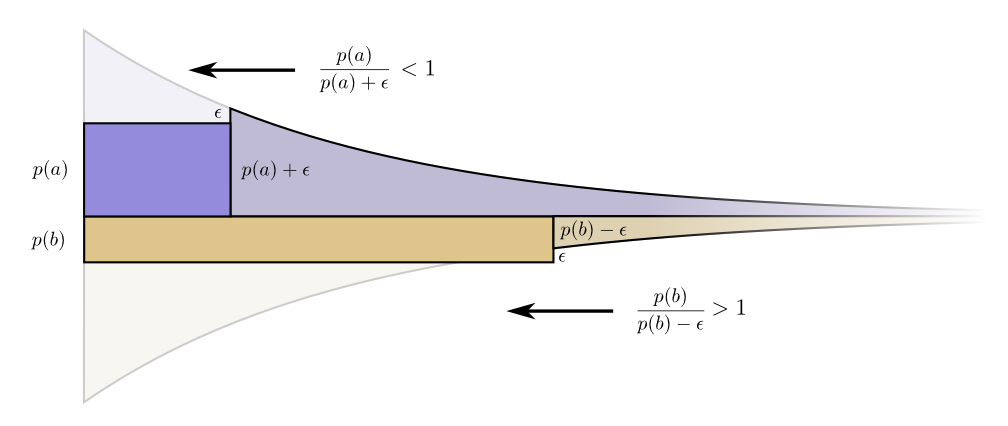
代价不再是平衡的了。把预算投给$b$比投给$a$更好。投资者会喊:买进$b$!卖出$a$!我们也这样做,最后就会回到我们最初的分配方案上。所有的预算分配方案都可以通过向我们之前提出的那个方案靠拢而变得更优。
我们最初的分配方案——即为每个码字分配的预算与它的使用频率成正比——不仅仅是一个自然而然的方案,更是一个最优的方案。(虽然上面的证明只考虑了两个码字的情况,但是推广到更多码字的情况是很容易的。)
(细心的读者可能已经注意到我们的最优分配方案有可能会使得某些码字具有非整数长度。这看起来很令人不安!这意味着什么?嗯,当然,在实践中如果你想要通过发送一个码字来进行交流,那么你必须对码字的长度进行四舍五入。但正如我们之后会看见的,有可能通过一次性发送多个非整数长度的码字来使得事情变得合理!现在先请你多一点耐心!)
熵的计算
回想起长度为$L$的码字的代价是$\dfrac{1}{2^{L}}$。我们把这个算式转换一下,得到给定代价下的码字长度为:$\log_{2}\left(\dfrac{1}{cost}\right)$。因为对于$x$的码字,我们所花费的代价是$p(x)$,所以该码字的长度就是$\log_{2}\left(\dfrac{1}{p(x)}\right)$。这就是码字长度的最佳选择。

在之前,我们讨论过,对于所用词汇服从某个特定概率分布$p$的通讯事件,信息的平均长度存在一个基本底限。这个限制,即使用最优编码时的平均信息长度,被称为$p$的熵,记为$H(p)$。现在我们知道了码字的最优长度如何确定,接下来我们就可以算熵了! $$\begin{aligned} H(p)=\sum_{x}p(x)\log_{2}\left(\frac{1}{p(x)}\right) \end{aligned}$$
(人们通常根据恒等式$\log(\frac{1}{a})=-\log(a)$把熵写为 $$\begin{aligned} H(p)=-\sum p(x)\log_{2}(p(x)) \end{aligned}$$ 我觉得我的写法更直观一些,所以在文章中我会使用我的写法。)
如果我想要能够用每个词汇进行交流,那么无论我如何努力,码字的平均长度都至少是那么多比特。
通讯信息所需的平均长度有时清晰地指明了对信息进行压缩的空间。除此之外我们还有什么理由去关心这个底限吗?当然有!这个底限描述了我对于事物的不确信程度,并且提供了一种对信息进行量化的方式16。
如果我确切地知道接下来会发生什么,那么我根本就不用通讯!如果存在两个事件,各自发生的概率都是50%,那么我只需要用1个比特进行通讯。但是如果有64个事件,它们发生的概率都相等,那么我就得用6个比特进行通讯17。概率分布越集中,我就越能找到一个良好的编码使得平均信息长度较短。概率分布越分散,我所发送的信息的平均长度就得越长。
一般来说,发生的事情越不容易确定,当发现究竟发生了什么时,我能学到的越多18。
交叉熵
在鲍勃搬到澳大利亚的不久前,他和爱丽丝(另一个我想象中的虚构人物)结婚了。使我和我脑海中的其他人物吃惊的是,爱丽丝不是一个狗狗爱好者。她更喜欢猫咪。尽管如此,他俩还是找到了共同点,就是都非常喜欢动物,同时词汇量也非常小。
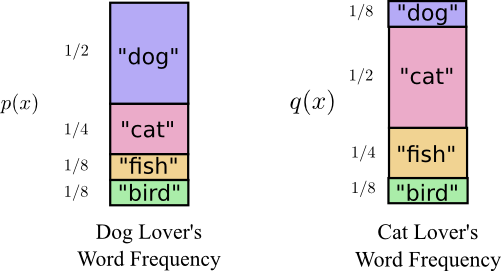
他们俩都使用同样的单词,只是使用各个词的频率不同。鲍勃喜欢谈论狗,而爱丽丝喜欢谈论猫。
刚开始,爱丽丝使用鲍勃的编码来向我发送消息。不幸的是,她的信息编码地有点浪费。鲍勃的编码对于他自己所用词汇的概率分布而言是最优的。爱丽丝所用的词汇有不同的概率分布,因此鲍勃的编码对于爱丽丝而言就可能不是最优的。用鲍勃的编码方式对鲍勃的消息进行编码,得到的码字的平均长度是1.75比特,而使用这种编码对爱丽丝的消息进行编码,得到的码字的平均长度是2.25比特。如果他们使用词汇的分布差异更大的话,得到的结果会更糟!
使用一种分布的最优编码对另一个分布进行编码,得到的码字的平均长度称为交叉熵(cross-entropy)。正式一点,我们可以作出如下定义19: $$\begin{aligned} H_{p}(q)=\sum_{x}q(x)\log_{2}\left(\frac{1}{p(x)}\right) \end{aligned}$$
在上述的例子中,我们得到的是在(喜欢狗狗的)鲍勃的词频下的(喜欢猫咪的)爱丽丝的词汇分布的交叉熵。

为了使我们通讯的成本降低,我请求爱丽丝使用她自己的编码。值得庆幸的是,这确实减小了她的信息的平均长度。但这也带来了一个新问题:有时候鲍勃会不小心用到爱丽丝的编码。出人意料地,鲍勃使用爱丽丝编码的情形比爱丽丝使用鲍勃编码的情形更糟!
所以,现在我们有四种可能性:
-
鲍勃使用他自己的编码($H(p)=1.75$比特)
-
爱丽丝使用鲍勃的编码($H_{p}(q)=2.25$比特)
-
爱丽丝使用她自己的编码($H(q)=1.75$比特)
-
鲍勃使用爱丽丝的编码($H_{q}(p)=2.375$比特)
仅凭直觉来考虑这里的情况并不容易20。比如,我们可以看到$H_{p}(q)\neq H_{q}(p)$。有没有一种方法可以让我们观察这四种情况彼此之间的联系呢?
在下图中,每一个子图都表示上述四种情况之一。在每一个子图中我们都使用曾经用过的方法来把平均信息长度表示出来。这些子图按照方块区域排列,使得并排的两幅图表示被编码的词汇来自同一个分布,而上下堆叠的两幅图表示使用的编码来自于同一个分布。这样使得你能够轻易地在不同的视角之间切换。
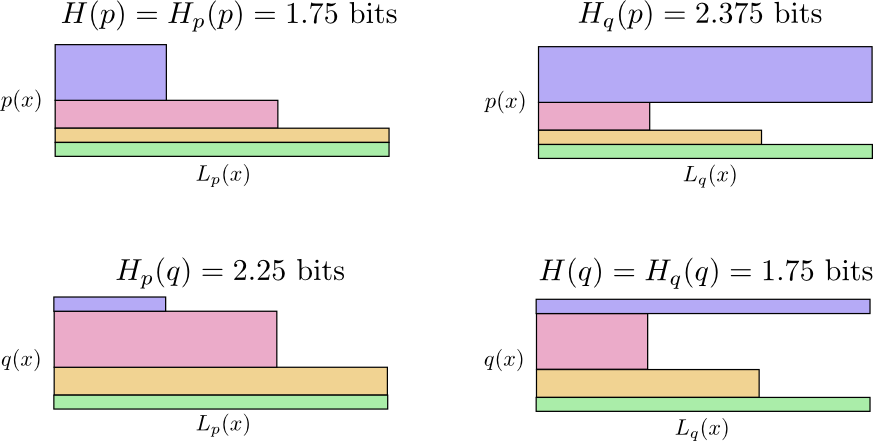
你能够看出为什么$H_{p}(q)\neq H_{q}(p)$吗?$H_{q}(p)$更大一些是因为存在一个词汇(蓝色)在$p$中很常用但是码字却很长,这是由于它在$q$的分布中很不常用。另一方面,在$q$中的常用词汇虽然在$p$中也不太常用,但是这个差异带来的影响较小,使得$H_{p}(q)$不会像$H_{q}(p)$那么大21。
因此交叉熵不具有对称性。
那么,为什么你应该关注交叉熵呢?嗯,交叉熵给了我们一种表达两个概率分布差异程度的方法。两个概率分布$p$与$q$的差异越大,$p$相对于$q$的交叉熵就会比$p$自身的熵大得更多。
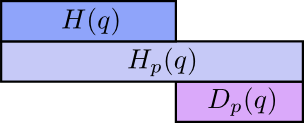
同样的,$p$与$q$的差异越大,也越会加剧$q$相对于$p$的交叉熵比$p$的熵大的程度。
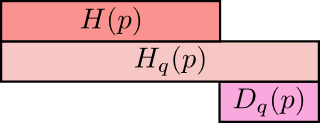
最有趣的地方在于熵与交叉熵之间的差。这个差代表着某个分布下的消息由于使用另一个分布下的编码,而额外使用的长度的平均值。如果这两个分布是相同的,那么这个差就是零。随着分布的差异变大,得到的差也会变大。
我们把这个差叫做库尔贝克-莱布勒散度(Kullback–Leibler divergence),或者简称为KL散度。$p$相对于$q$的KL散度记为$D_{q}(p)$22,它被定义为23: $$\begin{aligned} D_{q}(p)=H_{q}(p)-H(p) \end{aligned}$$
KL散度最优雅的地方在于它就像是两个分布之间的距离。它衡量了两者之间的差异有多大!(如果你仔细斟酌这个想法,最终你将会进入信息几何(information geometry)的领域 。)
交叉熵和KL散度在机器学习中是超级有用的。常见地,我们想让一个分布与另一个相接近。例如,我们会想让预测出来的分布和真实的分布相接近。KL散度给了我们一个自然的方式去达到这个目标,所以它被广泛地使用。
熵与多维变量
让我们回到之前的天气与穿衣的例子上来:
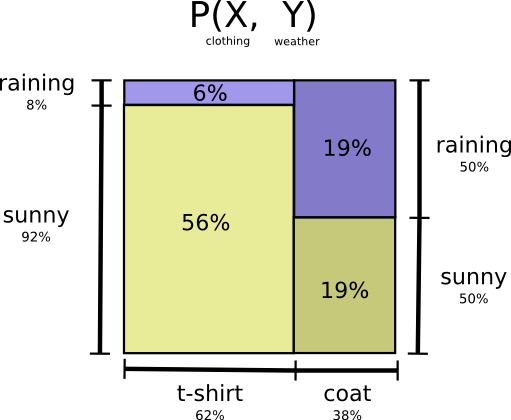
我的妈妈,就像大多数父母那样,时常担心我不好好穿衣服。(她的担忧是有道理的——我经常在冬天忘记穿外套。)所以,她经常想同时知道我所在地方的天气以及我正在穿的衣服。我需要用多少比特来把这些信息传输给她呢?
嗯,考虑这个问题的一个简单方式是把概率分布拉直:
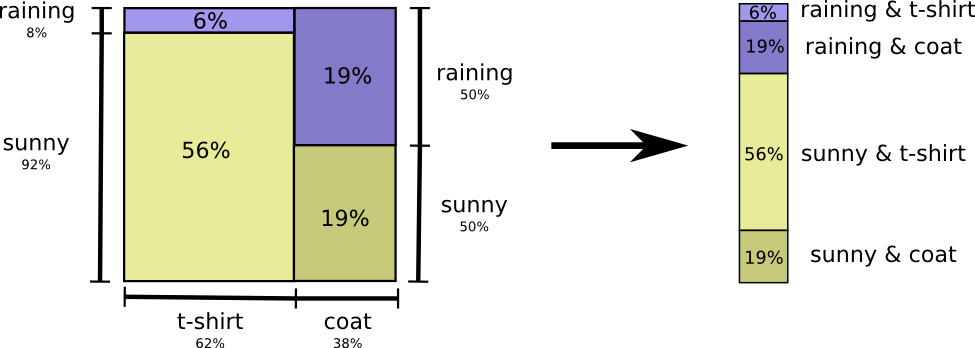
现在我们可以得出这些事件对应的最优码字,并且可以算出平均消息长度:
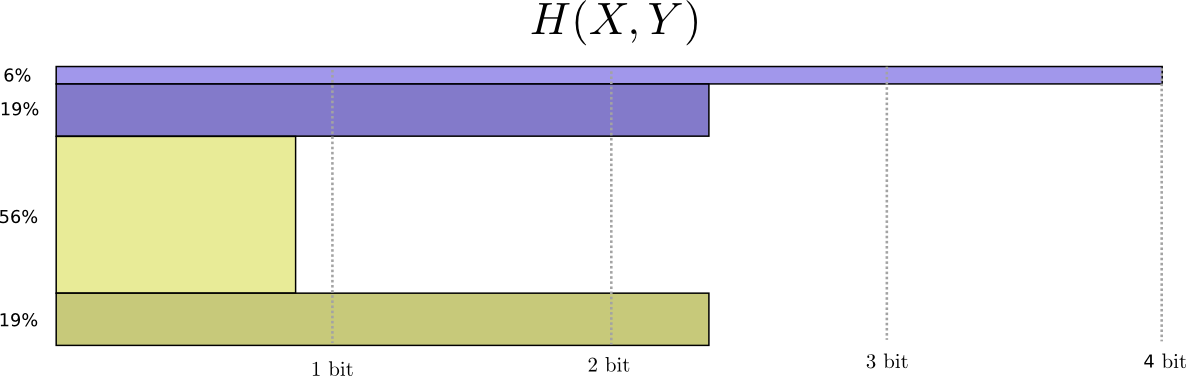
我们把这称为$X$和$Y$的联合熵,定义如下:
$$\begin{aligned} H(X,Y)=\sum_{x,y}p(x,y)\log_{2}\left(\frac{1}{p(x,y)}\right) \end{aligned}$$这和我们通常的定义是一致的,除了使用二维变量代替一维变量。
一个更好地思考方式是不把概率分布拉值,而是把码字长度看成第三维。现在熵可以用体积来表示!

但是假如我妈已经知道了天气情况。她可以从新闻中知晓。那么现在我需要提供多少信息呢?
看起来我似乎还是得把我穿什么衣服的信息完整地发出去24。但事实上我需要传送的信息量可以少一些,因为天气信息强烈地暗示了我将会穿什么衣服!我们来分别考虑雨天和晴天的情况。
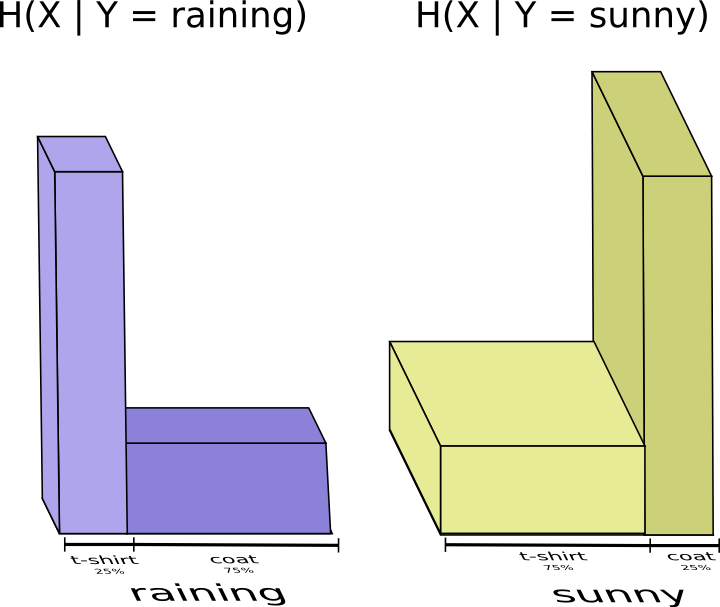
在这两种情况下,通常我都不必发送太多的信息,因为天气情况让我能够很好地猜测正确的答案是什么25。当天气晴朗时,我可以使用特制的晴天最优编码,当下雨时,我可以使用雨天最优编码。在两种情况下,我都比使用通用编码发送了更少的信息。要计算我给我妈发送信息的平均长度,我只需要把两种情况合在一起…

我们把这称为条件熵。如果你把它形式化成一个等式,会得到: $$\begin{aligned} H(X|Y) = & \sum_{y}p(y)\sum_{x}p(x|y)\log_{2}\left(\frac{1}{p(x|y)}\right) \\ = & \sum_{x,y}p(x,y)\log_{2}\left(\frac{1}{p(x|y)}\right) \end{aligned}$$
互信息
在上一节中,我们观察到,知道一个变量的情况意味着传输另一个变量所需的信息量变少了。
一个很好的理解方式是把信息量想象成一个长条。如果不同变量的信息之间有共享的部分,那么相应的信息条会有部分重叠。例如,$X$和$Y$之间存在着一些共享的信息,因此$H(X)$和$H(Y)$对应的信息条会有部分重叠。由于$H(X,Y)$是两者的信息量之和,所以把$H(X)$和$H(Y)$对应的信息条合并起来就得到$H(X,Y)$对应的长条26。
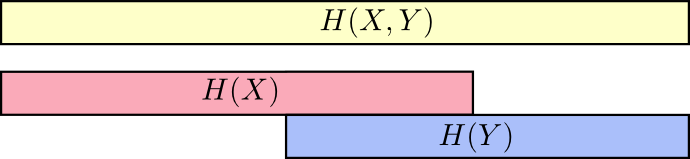
当我们开始这样思考问题,许多事情都变得简单了。
比如,我们之前提到同时传输$X$和$Y$(联合熵$H(X,Y)$)比只传输$X$(边缘熵(marginal entropy)$H(X)$)需要更多的信息量。但是一旦你已经知道$Y$的情况了,那么传输$X$的所需的信息量(条件熵$H(X|Y)$)将会更少!

这听起来有点复杂,但如果我们从信息条的角度来考虑就将变得很简单。$H(X|Y)$是向某个已经知道$Y$的情况的人传输$X$的情况所需要使用的信息量。同时,这也是$X$中不被$Y$所包含的信息量。从图形上看,这意味着$H(X|Y)$是$H(X)$的信息条中不与$H(Y)$的信息条相重叠的部分。
那么现在你就能从下面这个图中直接看出不等式$H(X,Y)\geq H(X) \geq H(X|Y)$
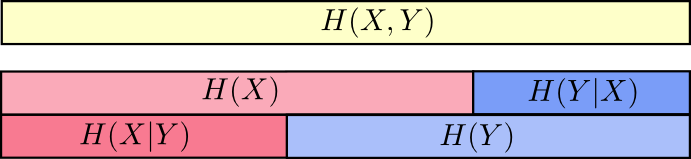
另外一个成立的等式是$H(X,Y)=H(Y)+H(X|Y)$。这表达的是,$X$和$Y$所共同包含的信息量等于$Y$的信息量加上$X$中不被$Y$所包含的信息量。
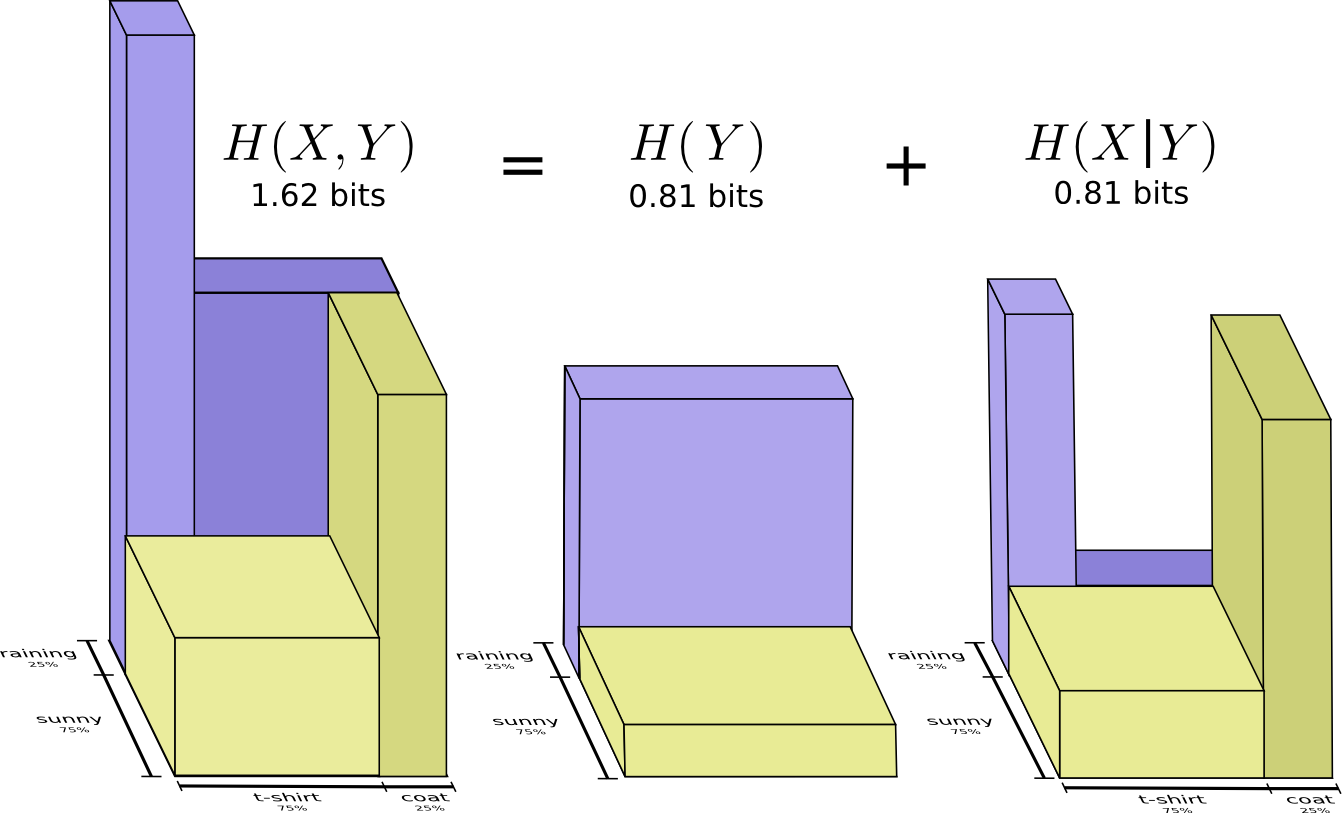
同样,抽象地去理解这个等式有点困难,但是如果我们从信息条堆叠的角度来理解就会容易得多。
到现在,我们对$X$和$Y$的信息量进行了不同角度的理解。我们讨论了单个变量的信息量$H(X)$和$H(Y)$。也讨论了两个变量联合起来的信息量$H(X,Y)$。还讨论了仅存在与单者中的信息量$H(X|Y)$和$H(Y|X)$。这些角度似乎都与两个变量之间共享的信息量(信息量的交)紧密相关。我们把共享的信息量称为“互信息(mutual information)”,记为$I(X,Y)$,定义为27: $$\begin{aligned} I(X,Y)=H(X)+H(Y)-H(X,Y) \end{aligned}$$
这样的定义之所以行得通,是因为$H(X)+H(Y)$包含了两份互信息($X$和$Y$中都有一份),而$H(X,Y)$只包含了一份。(从上面的条状图中可以看出来。)
与互信息相关的另一个概念是变信息(variation of information)。变信息是不被两个变量所共享的信息。我们可以把它定义成: $$\begin{aligned} V(X,Y)=H(X,Y)-I(X,Y) \end{aligned}$$
变信息是令人感兴趣的,因为它给了我们对于两个变量的度量,或者说一种距离的概念。当知道一个变量的值就能确定另一个变量的值时,二者的变信息为零。当两个变量变得越来越独立时,它们的变信息会越来越大。
变信息和KL散度(也可以看作是一种距离)有什么关联呢?嗯,KL散度告诉我们的是同一个(组)变量在不同分布间的距离,而变信息告诉我们在同一个联合分布中的两个变量间的距离。KL散度是分布间的,变信息是分布内的。
我们可以把上述所有关于信息量的概念放在下面这幅图中:

分数比特
在信息论中,一个非常不直观的事情是信息量可以是分数28。这真是太奇怪了。半个比特意味着什么?
这里有一个简单的回答:通常来说,我们关心的是消息的平均长度而不是某个消息的具体长度。如果在一半的情况下某人发送一个比特,而在另一半的情况下发送两个比特,那么他平均发送的就是1.5比特。平均数是一个分数这没什么奇怪的。
这个回答其实是在回避问题。我们经常可以看见最优码字长度是一个分数。这又意味着什么?
具体一点,让我们来考虑这样一个概率分布,事件$a$出现的时间占71%,事件$b$出现的时间占29%。
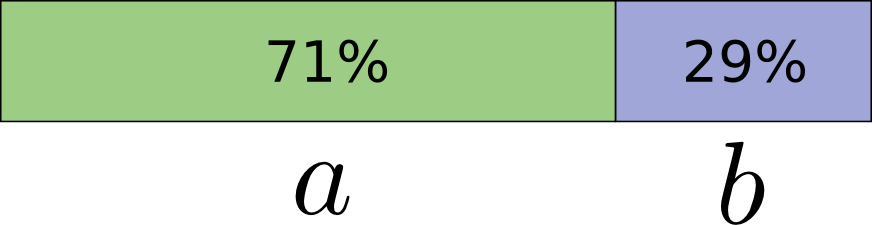
$a$对应的最优码字长度为0.5比特($\log_{2}(\frac{1}{0.71})\approx0.5$),$b$的为1.7比特($\log_{2}(\frac{1}{0.29})\approx 1.7$)。嗯,如果我们想要只发送一个码字,那么会出点问题。我们不得不把码字的长度取整,这样使得发送的平均长度变成1比特29。
…但是如果我们打算一次性发送多条信息,那么我们可以做得更好一些。让我们考虑在这个分布下发送两个事件的信息。如果我们每个事件的信息都单独地发送,我们还是得传输两个比特。我们可以做得更好一些吗?
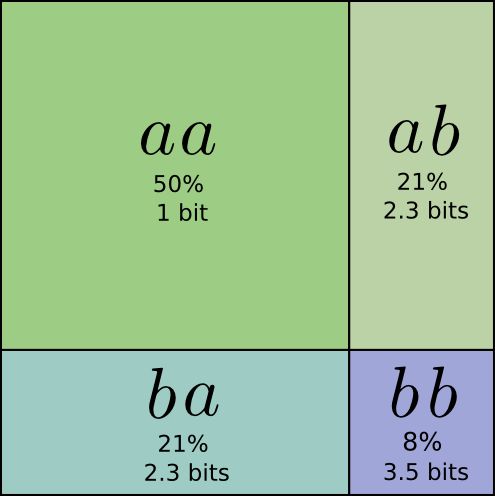
有一半的时间,我们会发送$aa$,发送$ab$和$ba$的可能性都是21%,而在8%的时间内我们会发送$bb$。再一次的,我们得出的理想码字长度还会是分数。
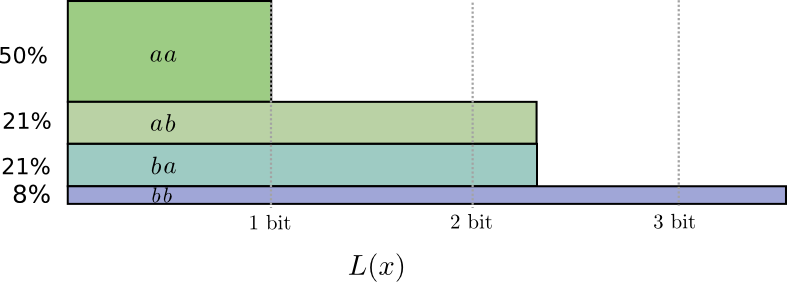
如果我们把码字的长度取整,会得到这样的结果:
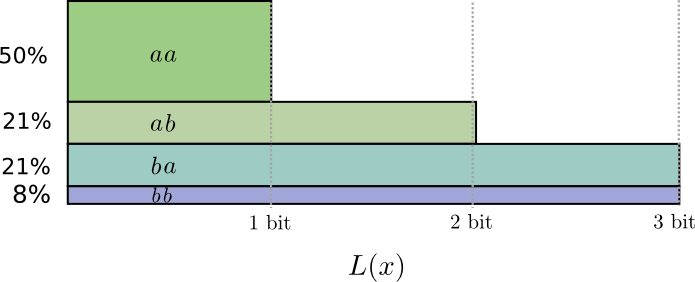
这个编码使得平均信息长度为1.8比特。这比单独发送消息时所需的2比特小一些。另外一种考虑方式是我们现在平均以0.9比特的长度发送每一个事件的信息。如果我们一次性发送更多事件的信息,那么码字的平均长度还会减少。当$n$趋向于无穷大时30,由于对码字长度进行取整所带来的开支就趋于零,并且码字的平均长度也趋向于熵。
进一步地,我们注意到$a$的理想码字长度是0.5比特,而$aa$的理想码字长度是1比特。理想码字长度是可以累加的,即使它是个分数!所以,如果我们一次性发送多个事件的信息,我们可以通过累加的方式得到新的理想码字长度31
虽然具体的码字长度必须是个整数,但是信息量是一个分数确实是可能的!
(实际上,在不同的领域人们使用不同的特定编码方案。比如我们之前在讨论的实际上是哈夫曼编码(Huffman coding),它无法优雅地处理分数比特的情况——就像我们之前做的那样,得把不同的码字合并成一组来处理,或者使用其它的技巧来接近熵。算数编码(Arithmetic coding)就有点不同,它能通过渐进最优的方式来优雅地处理分数比特32。)
总结
如果我们关心的是使用最少的比特来进行通讯,那么上述的概念无疑是非常有用的。如果我们关心的是数据压缩,信息论阐明了其中的关键问题并且把它很好地抽象了出来。但是如果我们都不关心这些,那么除了好奇心之外,我们还有什么理由去了解信息论吗?
信息论的概念其实在很多领域中都会用到,比如机器学习,量子物理,遗传学,热力学,甚至可以用在赌博中。这些领域的从业者可并不是因为关心数据压缩所以要了解信息论,而是因为信息论与他们从事的领域有紧密的联系。用熵可以很好地解释量子纠缠33。许多在统计力学和热力学中的结论可以通过假设未知的事物的最大熵来推出。一个赌徒的输赢与KL散度有着直接的关联34,特别是在不停地下注的时候35。
信息论之所以在上述领域中有所应用,是因为它能够对人们想要表达的许多事情进行具体而又准确的描述。它给予我们衡量和表达不确定性的方法,能够告诉人们两组判断有多少不同,还能让我们通过一个问题的答案知道更多关于:概率分布有多分散,两个概率分布间的距离是多少,以及两个变量之间的独立性有多少。有其它相似的概念能够做到这些吗?当然有。但是信息论所提供的概念非常的清晰,具有优美的性质,同时还有良好的理论基础。在某些情况下,它能够精确地表达你所关心的事物,在另一些情况下,它能够让你方便地对真实世界进行抽象。
机器学习是我最了解的领域,所以让我们再多谈一点。机器学习里最常见的任务就是对事物进行分类。比如我们想要观察一张图片,然后判断图片的内容是狗还是猫。我们设计的模型可能会说:“有80%的可能性这是一张关于狗的图片,而是猫的概率是20%。”让我们假设正确答案就是狗,那么我们的预测——有80%的可能性是狗——有多好或者多坏呢?如果有一个新的预测结果是那副图有85%的可能性是狗,那么新的预测比原来的预测好多少呢?
这是一个很重要的问题,因为如果我们想对模型进行优化,那么就需要有一种概念来衡量模型的好坏。我们如何去优化呢?这取决于我们的模型是用来干什么的:我们是只关心最好的预测结果是否正确?还是只关心对于正确的答案我们有多少的确信度36?当我们预测错误时局面会有多糟糕呢?很难去回答这个问题。而且通常情况下我们无法知道会有多糟,因为我们不知道模型是否运作地和我们设想的一致37。结果就是,在某些情况下,交叉熵正好能衡量模型的好坏,而在另外一些情况下则不行。很多时候我们无法确定模型的预测重点38,即便如此,交叉熵仍然是一个不错的抽象工具39。
从信息的角度来看待事物为我们提供了一种有效的思维框架。有时候它能够很好地处理我们的问题,但有时候可能不行,不过它依然非常有用。这篇文章只是触及了信息论的皮毛——有许多重要的话题,例如错误纠正编码(error-correcting codes),没有被提及——但是我希望它向大家展示了信息论是一个美妙的学科,我们无需对它望而却步。
如果你愿意帮助我成为一个更好的写作者,请填一下这个反馈表,让我听听你的意见。
延伸阅读
Claude Shannon对于信息论的开创性论文 A Mathematical Theory of Communication是非常易读的。(似乎在早期的信息论文献里有着重复的论证。这是那个时代的风格吗?还是说因为纸多?还是说这是贝尔实验室的文化40?)
Cover和Thomas的著作Elements of Information Theory是信息论领域的标准参考书。我个人认为它是有用的。
致谢
非常感谢Dan Mané, David Andersen, Emma Pierson和Dario Amodei付出时间为我的文章作出细致的评论。此外我还要谢感Michael Nielsen, Greg Corrado, Yoshua Bengio, Aaron Courville, Nick Beckstead, Jon Shlens, Andrew Dai, Christian Howard, 以及Martin Wattenberg对文章作出的评论。
同样感谢我最初参与的两个神经网络系列研讨课,在那之中我对我的想法进行了尝试41。
最后,感谢为文章挑出错误和疏忽的读者们。特别要感谢Connor Zwick, Kai Arulkumaran, Jonathan Heusser, Otavio Good, 以及一位匿名的评论者。
- 1.原文为:How uncertain am I? How much does knowing the answer to question A tell me about the answer to question B? How similar is one set of beliefs to another? ↩
- 2.原文为:I’ve had informal versions of these ideas since I was a young child, but information theory crystallizes them into precise, powerful ideas. ↩
- 3.通过这种方式来把天然带有独立性的朴素贝叶斯分类器进行可视化是很有趣的。 ↩
- 4.译者注:有人可能会说,其实是可以确定下来的,因为如果第一个码字是“0”,那么接下来的编码字符串“100111”就无法再进行翻译了。但是在解码的时候,这样的做法太低效了,需要去判断很多事情。为了提高解码的效率,一般的做法就是不停地读入字符串,一旦能够确定一个码字,就立刻把它解码。所以我们才需要之后提到的前缀编码。 ↩
- 5.原文为:The property we want is that if we see a particular codeword, there shouldn’t be some longer version that is also a codeword. ↩
- 6.译者注:“有限的预算”想表达的意思应该就是说不能随意地使用码字空间。或者说,我们的预算就是1,代表整个码字空间,我们要合理地用掉这个预算,使得平均编码长度尽可能地小。这里应该隐含着一个意思,就是预算一定得用完,即把整个码字空间都消耗掉。 ↩
- 7.原文为:You can think of this like having a limited budget to spend on getting short codewords. We pay for one codeword by sacrificing a fraction of possible codewords. ↩
- 8.在这里我处理得不太精确。在图中我用的是以2为底的指数,这并不能得到高度和面积一致的结论,所以我在叙述的时候补充上了自然指数的限制。这样的处理方式使得接下来的证明中省去了很多$\log(2)$,同时也让我们的图形变得好看一些。 ↩
- 9.译者注:这里说的实际上就是一个等量替换,事实上cost应该就是$cost=2^{-L(x)}$曲线上的对应点,但是作者把它和深色部分的面积等同了,这在曲线是$cost=e^{-L(x)}$的情形下是成立的,因为深色部分的面积是$\int_{L(x)}^{\infty}e^{-L(x)}=e^{-L(x)}=cost$,而当曲线是$cost=2^{-L(x)}$时,那样的等量代换就不成立了,因为$\int_{L(x)}^{\infty}2^{-L(x)}=\dfrac{-1}{\ln 2}2^{-L(x)}=\dfrac{-1}{\ln 2}cost$。作者说的$\log(2)$应该是指$\ln(2)$。 ↩
- 10.译者注:应该就是指如何合理地使用码字空间。 ↩
- 11.原文为:What’s the best way to use our limited budget? How much should we spend on the codeword for each event? ↩
- 12.译者注:这里其实就是在说导数。虽然从图上看确实是那么个意思,但是我们还是来一点数学推算吧。首先,边界的高度在此处都是$p(a)$,对于平均信息长度,码字的长度贡献的计算公式是$L_{c}(a)=L(a)\times p(a)$,对$L(a)$求导,得到$\dfrac{\partial L_{c}(a)}{\partial L(a)}=p(a)$。对于码字代价,用自然指数的话,计算公式是$C(a)=e^{-L(a)}$,那么对应的导数是$\dfrac{\partial C(a)}{\partial L(a)}=e^{-L(a)}=C(a)$,等同于边界的高度。注意,两块区域的边界高度有一点区别,代表对平均信息长度贡献的区域的边界高度始终等于$p(a)$,而代表码字代价的区域的边界高度是随着码字的长度而改变的,是$e^{-L(a)}$,了解这一点对理解之后的论述是有益的。 ↩
- 13.译者注:应该就是变短1比特。 ↩
- 14.原文为:if you had a bit more to spend, it would be equally good to invest in making any codeword shorter. ↩
- 15.原文为:Infinitesimally, it doesn’t make sense to change the budget. ↩
- 16.原文为:The average amount of information needed to communicate something has clear implications for compression. But are there other reasons we should care about it? Yes! It describes how uncertain I am and gives a way to quantify information. ↩
- 17.译者注:指的是平均码字长度为6比特,$64\times\log_{2}\left(\frac{1}{64}\right)=6$。 ↩
- 18.译者注:这句话不知该如何翻译,我想大意就是当稀有的事情发生时,能提供更多的信息量,因为很可能存在其它因素导致了稀有事件的发生。原文为:The more uncertain the outcome, the more I learn, on average, when I find out what happened. ↩
- 19.提醒一下,使用$H_{p}(q)$来表示交叉熵不是标准的做法。通常使用的符号是$H(p,q)$。但是这个符号有两点不好:第一,联合熵(joint entropy)用的也是这个符号。第二,这个符号让人觉得交叉熵具有对称性。这显得有点荒唐,所以我用$H_{p}(q)$来替代。 ↩
- 20.译者注:这里不知道该如何翻译,原文 为:This isn’t necessarily as intuitive as one might think. ↩
- 21.译者注:其实也可以很直观地去解释:在$p$中,dog是最常用的词,cat是第二常用的词,在$q$中,cat是最常用的词,dog是最不常用(第四常用)的词。使用$p$的编码来编$q$的码字,会出现最常用的词的码字是第二短的,而用$q$的编码来编$p$的码字,会出现最常用的码字却是最长的!这就导致$H_{q}(p)$比$H_{p}(q)$大(当然准确地说还要考虑其它词汇,但是在这里考虑最常用的词汇就能说明问题)。 ↩
- 22.这也不是表示KL散度的标准符号。 ↩
- 23.如果你把KL散度的定义展开,将会得到$D_{q}(p)=\sum_{x}p(x)\log_{2}\left(\dfrac{p(x)}{q(x)}\right)$这看起来可能会有点奇怪。我们该如何解释它呢?嗯,$\log_{2}\left(\dfrac{p(x)}{q(x)}\right)$代表了使用为$p$优化的编码和为$q$优化的编码来表示$x$时所用比特数的差异。整体上看,表达式就是在计算两种编码得到的码字长度差异的期望 ↩
- 24.原文为:It seems like I need to send however much information I need to communicate the clothes I’m wearing. ↩
- 25.原文为:In both cases, I don’t need to send very much information on average, because the weather gives me a good guess at what the right answer will be. ↩
- 26.Raymond W. Yeung 在他的论文A New Outlook on Shannon’s Information Measures中阐述了这样的做法为信息论的集合解释建立了基础。 ↩
- 27.如果你把互信息的定义展开,将会得到$I(X,Y)=\sum_{x,y}p(x,y)\log_{2}\left(\dfrac{p(x,y)}{p(x)p(y)}\right)$这看起来和KL散度非常像!这是为什么呢?嗯,它确实就是KL散度。实际上,它是$P(X,Y)$和其简单近似$P(X)P(Y)$的KL散度。它表达了相比于假设$X$和$Y$是独立的,当确切地知道两者的关系时,对它们进行表达所能节约的比特数。一个好玩的展现方式是,把等式中的真实分布($p(x,y)$)和近似分布($p(x)p(y)$)用图片来替代:
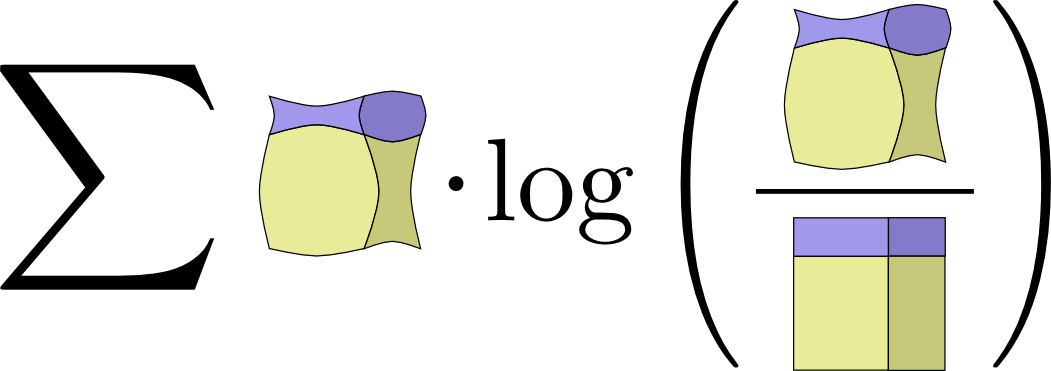 ↩
↩ - 28.原文为:A very unintuitive thing about information theory is that we can have fractional numbers of bits. ↩
- 29.译者注:把$a$和$b$的码字长度都变成1比特。在这里,取整不是简单地四舍五入或者只朝同一个方向取整,要结合编码的情况来考虑。 ↩
- 30.译者注:即发送一次信息中包含的事件数趋向于无穷多。 ↩
- 31.译者注:我猜想作者想要表达的意思就是,如果$a$的理想码字长度是0.5,$b$的理想码字长度是1.7,那么$ab$的理想码字长度就是0.5+1.7=2.2。可能需要一点具体的证明,不过从直觉上看,乘法在对数的作用下会变成加法,那样的做法应该是行得通的。 ↩
- 32.原文为:Arithmetic coding is a bit different, but elegantly handles fractional bits to be asymptotically optimal. ↩
- 33.作为一个统计物理的门外汉,我会很谨慎地概述一下在我理解中它与信息论的联系。在Shannon提出信息论之后,许多人意识到热力学和信息论中的一些公式有那么点相似。E.T. Jaynes发现了一个非常深刻而又严谨的联系。假设有一个热力学系统,它具有某些度量值,例如压力和温度。你会如何假设该系统处于某个状态的概率呢?Jaynes认为,我们应该假设度量值的概率分布具有最大的熵。(注意这里用到的“最大熵原理(principle of maximum entropy)”不仅仅存在于物理学中,它是常见的。)也就是说,我们所假设的概率分布要具有最多的未知信息。许多结论都能从这个视角得到。(参考Jaynes论文的前几节(第一部分,第二部分),这篇论文浅显易懂让我印象深刻。)如果你对这个联系感兴趣,但是又不想去读论文,那么可以去看Cover和Thomas的书,其中有一个章节通过马尔可夫链(Markov Chains)推导出了热力学第二定律的统计学版本! ↩
- 34.原文为:A gambler’s wins or losses are directly connected to KL divergence, in particular iterated setups. ↩
- 35.信息论和赌博的联系第一次被提及,是在John Kelly的论文A New Interpretation of Information Rate之中。虽然它需要一些在本文中未涉及的概念,但是仍不失为一篇非常易读的文章。Kelly进行这项研究的动机很有趣。他注意到熵被用于许多与信息编码无关的代价函数中,于是就想去探究该种用法的合理性。在写作本文时,我也遇到了同样的困惑,因此我非常感激Kelly的研究所提供的视角。然而,他的说法有点不让人信服:Kelly只是在赌徒会不停地把所有的资本作为赌注的情况下引出熵,在其它的下注策略下是得不到熵的。在Cover和Thomas的权威著作Elements of Information Theory中,有对Kelly观点的精彩论述。 ↩
- 36.原文为:Do we only care about whether the top guess was right, or do we care about how confident we are in the correct answer? ↩
- 37.原文为:There isn’t one right answer to this. And often it isn’t possible to know the right answer, because we don’t know how the model will be used in a precise enough way to formalize what we ultimately care about. ↩
- 38.原文为:Much more often we don’t know exactly what we care about and cross-entropy is a really nice proxy. ↩
- 39.虽然无法解决问题,但是我在这里还是忍不住想提一下KL散度。在Cover和Thomas的书中用到了一个Stein引理(Stein’s Lemma),不过这和我们通常说的Stein引理不是同一件事。概括地说,这个Stein引理讲的是:假设你有了一些观测数据,这些数据来自某两个概率分布中的一个。你能多确信是哪个概率分布产生了这些数据呢?一般而言,随着你获得的数据越来越多,你对于判断的确信程度是呈指数上升的。比如说,平均而言,每获得一个新数据,你对于自己判断的正确性的确信程度就会上升1.5倍。确信度的上升速度取决于两个分布的差异程度。如果两个分布差异很大,你可以很快地把答案确定下来。但是如果它们很相似,那么你可能需要采集大量数据之后才能得到一个稍微可靠的判断。Stein引理说的就是,粗略地看,置信度的乘数因子是由KL散度控制的。(这与假正例(false-positives)和假负例(false-negatives)之间的权衡有点微妙的联系(此处原文为:There’s some subtlety about the trade off between false-positives and false-negatives.)。)这看起来是一个让我们重视KL散度的好理由! ↩
- 40.原文为:This seems to be a recurring pattern in early information theory papers. Was it the era? A lack of page limits? A culture emanating from Bell Labs? ↩
- 41.原文为:Thanks also to my first two neural network seminar series for acting as guinea pigs for these ideas. ↩
- 文章标题: 直观理解信息论
- 文章作者: undefined
- 发布时间: 一月 2日 2017, 3:20 下午
- 最后更新: 三月 11日 2023, 9:39 晚上
- 本文字数: 本文一共有14,740字
- 原始链接: https://chenyangyu.top/2017/01/02/visual-information-theory/
- 许可协议: 自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
转载请保留以上信息。
